Continuous Trajectory Generation Based on Two-Stage GAN

杨镇源 于 2024-03-30 发布 浏览量

Continuous Trajectory Generation Based on Two-Stage GAN

原文

一、Abstract

本文提出了一个新颖的两阶段生成对抗框架来生成道路网络上的连续轨迹，即TS-TrajGen，它有效地将人类移动领域知识与无模型学习范式相结合。

具体来说，我们根据A*算法的人类移动假设构建生成器来学习人类移动行为。对于鉴别器，顺序奖励（sequential reward）和移动偏航奖励（mobility yaw reward）结合在一起，以增强生成器的有效性。

最后，我们提出了一个新颖的两阶段生成过程，以克服现有随机生成过程的弱点。

二、Introduction

生成合成且逼真的轨迹的重要性：

  1. 合成轨迹对于城市规划、疫情传播分析和交通控制至关重要
  2. 生成合成轨迹是保护人类移动轨迹数据隐私的可行解决方案

当前模拟人类移动轨迹存在的问题:

-> 提出无模型方法,使用神经网络生成范式，如生成对抗网络和变分自动编码器

存在问题：

然后文章大致介绍了基于A*假设，这里提出的方法是如何解决上述三个问题的。

首次通过将A*算法与神经网络相结合来解决城市道路网络上的连续轨迹生成问题。

三、Preliminary

轨迹定义： 一个时间顺序序列$T={x_1,x_2,…,x_n}$，其中$x_i$是一个元组$(l_i,t_i)$，$l_i$指示位置（道路段ID），$x_i$指示时间戳

连续轨迹定义： 指的是序列中的相邻元素$x_i,x_{i+1}$指示的道路段$l_i, l_{i+1}$在路网中是相邻的

Continuous Mobility Trajectory Generation： 给定一个真实世界的移动轨迹数据集，通过一个$\Theta$参数化的生成模型$G$生成一个连续的移动轨迹 $\hat{T} = {\hat{x_1}, \hat{x_2},…, \hat{x_n}}$

事实上，这是一个马尔可夫决策过程（MDP），记现有状态$s$由$x_{1:i}$组成，给定目标道路段$l_d$，下一步道路段选择为$l_{i+1}$（行动记为$a$），那么运动策略实际上建模为 $\pi(a\ given\ s)$

Human Movement Policy：

\[\pi(a\ given\ s)=P(a\ given\ s)=P(l_{i+1}\ given\ x_{1:i}\cap l_d)\]

生成过程可以描述为将以下生成轨迹的概率最大化：

\[\hat{T}=\max\prod\limits_{i=1}^n\pi(a_i\ given\ s_i)=\max\limits_{P_\Theta}\prod\limits_{i=1}^nP_\Theta(l_{i+1}\ given\ x_{1:i}\cap l_d)\]

四、The Proposed Framework

生成器$G$： 学习人类移动策略 $\pi(a\ given\ s)$

判别器$D$： 生成奖励$R$以引导生成器的优化过程

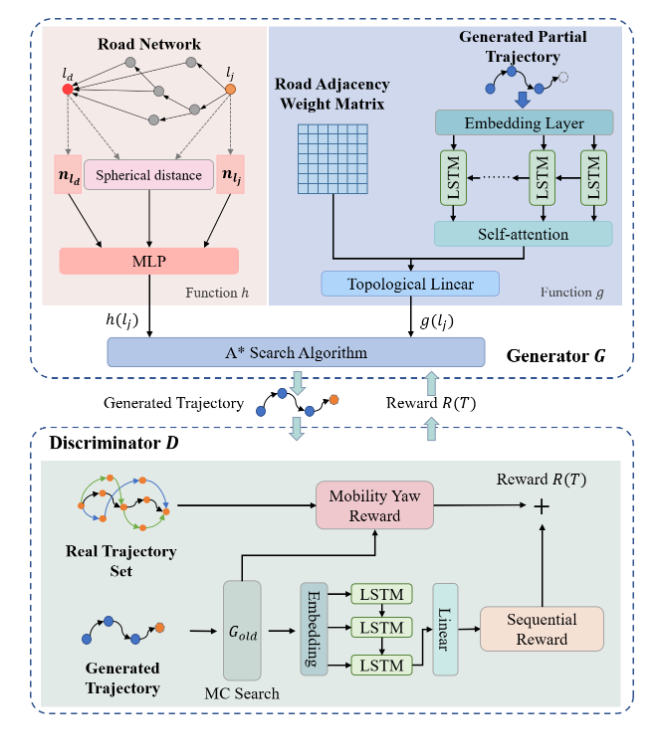
生成器和判别器

根据前文定义Human Movement Policy，为考虑当前部分轨迹和旅行目的地的影响，采用A*来建模人类移动策略 $\pi(a\ given\ s)$

$f(l_j)=g(l_j)+h(l_j)$，$g(l_j)$评估当前部分轨迹的观察成本，$h(l_j)$估计通过候选道路$l_j$到达目的地$l_d$的预期成本

\[f(l_j)=-\log\pi(a\ given\ s)=-\log P(l_j\ given\ x_{1:i}\cap l_d)\]

单纯使用A*存在不足：

因此，在本文中使用神经网络来实现$g$和$h$

4.1 Function $g$

结合LSTM网络和自注意机制，对当前的观察成本进行建模，学习当前的运动状态。

使用拓扑约束的线性层来预测观察到的成本：

  1. 给定当前部分轨迹$x_{1:i}$，将它的时空信息$(l_i,t_i)$嵌入到稠密向量中，即

    \[x_i=Embed(l_i)||Embed(encode(t_i))\]

  2. 将当前的部分轨迹转换为一系列稠密向量${x_1, x_2,…, x_i}$。接着，使用LSTM网络来建模顺序轨迹的运动状态${h_1, h_2,…, h_i}$。进一步利用点积注意力机制来增强潜在的移动状态$\widetilde{h_i}$的形式为：

    \[\widetilde{h_i}=\sum\limits_{k=1}^i att(h_i, h_k)\cdot h_k\]

    其中函数$att(·,·)$通过点积方法评估当前移动状态$h_i$与历史移动状态$h_k$之间的相关权重

  3. 最后，在捕获增强的移动状态之后，构建一个拓扑约束的线性层来预测观察到的条件概率$P(l_j\ given\ x_{1:i})$。在拓扑约束的线性层中，引入拓扑邻接权重$adj_{l_i,l_j}$到线性层中，当候选道路$l_j$与当前道路$l_i$相邻时为1，否则为0。利用拓扑邻接权重，将非相邻候选道路$l_j$的条件概率$P(l_j\ given\ x_{1:i})$设为零，以确保生成轨迹的连续性

    \[P(l_j\ given\ x_{1:i})=\frac{exp(\omega_{l_j}\cdot \widetilde{h_i}\cdot adj_{l_i,l_j})}{\sum_{l_k}exp(\omega_{l_k}\cdot \widetilde{h_i}\cdot adj_{l_i,l_k})}\]

观测成本$g(l_j)=-\log P(l_j\ given\ x_{1:i})$

4.2 Function $f$

图注意力网络从道路网络中提取相对位置信息，并计算两个道路段之间的球面距离。基于上述信息使用多层感知器网络来估算预期成本$h$。

  1. 首先构建图注意力网络来学习包含相对位置信息的结构道路表示。图注意力网络的更新可以表示为：

    \[N^{(z+1)}=GAT(N^z, A)\]

    $N^z\in R^{|L|\times d_s}$，是道路矩阵迭代$z$次的结果，$l_i-th$行$n_{l_i}\in R^{d_s}$与道路段$l_i\in L$相对应，$A$是路网的邻接矩阵

  2. 在获得$N^z$后，使用多层感知网络来预测从候选道路$l_j$到目的地$l_d$的预期条件概率，表示为：

    \[P(l_j\ given\ l_d)=MLP(n_{l_j},n_{l_d},d_{l_j,l_d})\]

    $n_{l_j}$和$n_{l_d}$分别是道路$l_j$和$l_d$在$N^z$中的表示，$d_{l_j,l_d}$是它们之间的球面距离

  3. 预期成本$h(l_j)=-\log P(l_j\ given\ l_d)$

Remark: 与原始的A*算法相比，上述方法能在引入时间信息和顺序运动状态的情况下对不同的人类运动策略进行建模，此外结合结构道路表示，提高了预期成本$h(l_j)$的有效性

4.3 Enhancing Generator with Discriminator

一般来讲，生成对抗网络学习使用的最小最大竞赛如下：

\[\min\limits_\Theta\max\limits_\Phi E_{\textbf{x}\sim p_d}[\log D_{\Phi}(x)]+E_{\textbf{x}\sim G_\Theta}[\log(1-D_\Phi(x))]\]

其中$\textbf{x}\sim p_d$表示从真实数据分布中抽取的样本，$\textbf{x}\sim G_\Theta$表示由生成器生成的样本，而$D_\Phi$是参数化为$\Phi$的鉴别器。鉴别器$D_\Phi$的目标是区分输入样本，生成器$G_\Theta$根据鉴别器的输出信号即奖励$R$来优化自身

$R(T)=R_s(T)+R_m(T)$

4.4 Two-Stage Generation Process

提出问题：随机生成轨迹过程存在误差累积问题，一旦生成器预测错误，随机生成过程将在错误的前提状态下继续生成。特别是在生成长轨迹时，随着生成器的预测次数增加，生成器出错的概率也会增加。这使得到达目的地变得困难，并降低了生成轨迹的质量。

论文提出的解决方案：基于A*搜索的新颖的两阶段生成过程

生成区域轨迹的算法：

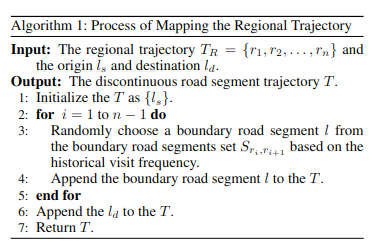
4.5 Training Process

这一部分讲解了对函数$g,h$的训练过程，看不太懂

五、Experiment

论述了自己这个模拟方法如何验证优越性：与其他五个模拟器进行比较

（这里可以看一看引用的论文做了什么工作）